Location General Setting Accomodation Speakers Organization team Program Abstracts
Dates: from March 18th to 20th, 2025.
Location
The conference is held at the University of Pau and Pays de l’Adour, in the Présidence Room.

Accomodation
Here you will find a few suggestions for hotels, although there are plenty more.
General setting
The Journées Ondes du Sud-Ouest are an opportunity to bring together researchers from south-west France who are contributing to the simulation of wave propagation phenomena. Topics covered range from mathematical modeling to the implementation of resolution algorithms in advanced computing environments. The integration of artificial intelligence methods and the use of accelerator technologies are also important topics. Particular attention is paid to applications including, but not limited to, defense, aeronautics, underground exploration and medical imaging. These meetings have been held since 2016, and are co-organized by CEA Cesta, Onera and the Inria center at the University of Bordeaux, three research centers that are very active in this field. The aim of this event is to create and/or strengthen collaborations on a regional and national scale, but also to raise awareness among the local network of SMEs - particularly dynamic in the Nouvelle Aquitaine and Occitanie regions - of the issues involved in numerical simulation on waves, and of the innovation capabilities of public laboratories in the South-West in this field.
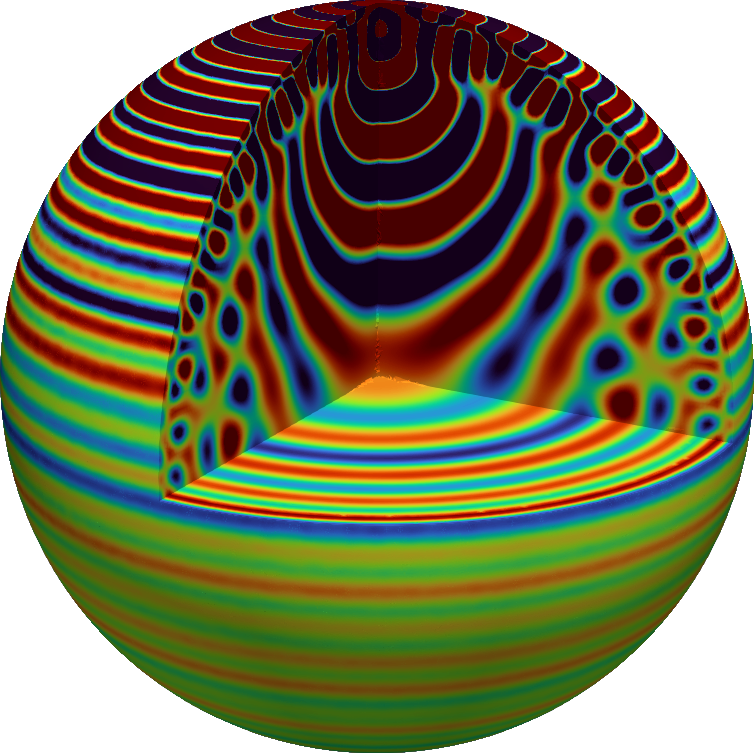
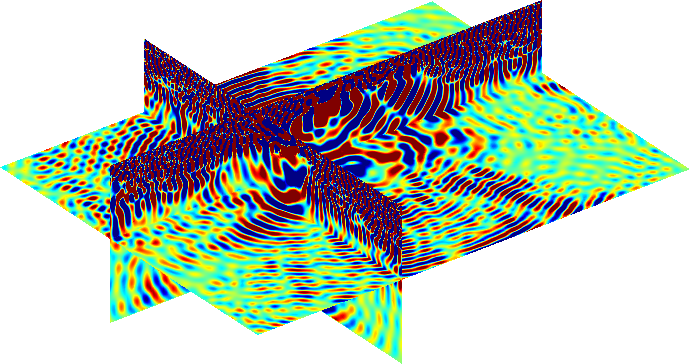
Courtesy of F. Faucher (Inria Makutu), open-source software Hawen .
Keynote Speakers
-
Frédéric Alauzet (Inria, GammaO)
-
Martin Gander (Université de Genève)
-
Laure Giovangigli (POEMS, CNRS, Inria, ENSTA Paris, Institut Polytechnique de Paris)
Organization Committee
-
Emmanuele Arcese (CEA Cesta)
-
Hélène Barucq (Inria Makutu)
-
Matthieu Lecouvez (CEA Cesta)
-
Sébastien Pernet (Onera Toulouse)
-
Ha Pham (Inria Makutu)
Program
Tuesday, March 18th |
|
| 12:00 -- 13:40 | Welcome Lunch at University restaurant La Vague |
| 13:40 -- 13:45 | Conference introduction |
| 13:45 -- 14:15 | Xavier Ferrières, "Time Schemes for Solving Maxwell's Equations in a Mesh Hybridization Strategy" |
| 14:15 -- 14:45 | Lola Chabat, "Wave and spectral solvers with self-gravitation for radially symmetric adiabatic backgrounds in helioseismology" |
| 14:45 -- 15:30 | Coffee break for Discussion |
| 15:30 -- 16:00 | Guillaume Sylvand, "Recent Developments in Waves Simulation at Airbus" |
| 16:00 -- 16:30 | Marie Bibal,"The importance of an efficient Helmholtz solver for modelling plasma discharges at atmospheric pressure" |
| 16:30 -- 17:00 | Matthias Rivet, "A Quasi-Trefftz Method for the Iterative Solution of Time-Harmonic Wave Problems based on the Flux Reconstruction Method" |
Wednesday, March 19th |
|
| 8:30 -- 9:30 | Laure Giovangigli, "Wave propagation in random multi-scale media and quantitative ultrasound imaging" |
| 9:30 -- 10:00 | Ilyes Moufid, "Optimization of equivalent circuit models for metal-patterned metasurfaces" |
| 10:00 -- 10:45 | Coffee break for Discussion |
| 10:45 -- 11:15 | Olivier Lafitte, "Asymptotic expansion and pseudodifferential calculation methods for wave propagation and reflection in a harbor" |
| 11:15 -- 11:45 | Edouard Demaldent, "1st kind BEM applied to non-destructive eddy current testing" |
| 11:45 -- 12:30 | Poster Session |
| 12:30 -- 13:45 | Lunch at University restaurant La Vague |
| 13:45 -- 14:45 | Martin Gander, "Best Current Parallel in Time Methods for Parabolic and Hyperbolic Problems" |
| 14:45 -- 15:15 | Pierre-Henri Cocquet, "Dispersion correction for finite difference approximations of Helmholtz equation" |
| 15:15 -- 16:00 | Coffee break for Discussion |
| 16:00 -- 16:30 | Jean-René Poirier, "Fast solution of a nonlinear eigenvalue problem from photonic crystal fiber applications discretized by a boundary element method" |
| 16:30 -- 17:00 | Vincent Perrier, "Conservation of divergence or rotational type constraints of hyperbolic systems with the discontinuous Galerkin method" |
| 19:30 | Conference Dinner |
Thursday, March 20th |
|
| 9:15 -- 10:15 | Frédéric Alauzet, "Impact of anisotropic mesh adaptation for turbulent flows in aeronautics. Towards the certification of numerical solutions ?" |
| 10:15 -- 11:00 | Coffee break for Discussion |
| 11:00 -- 11:30 | Mamadou N'Diaye, "Minimization of spurious reflections for non regular traveling waves on non uniform grids" |
| 11:30 -- 12:00 | Marc Bakry, "Full Helmholtz decomposition on non simply connected domains, application to 1st kind BEM for low-frequency electromagnetics" |
| 12:00 -- 12:30 | Matthias Barray, "Cancellation Integration Scheme for the Magnetic Boundary Integral Operator on Curved Elements and Application to the Accurate Computation of the Radar Cross Section" |
| 12:30 -- 14:00 | Buffet at University restaurant La Vague |
List of Abstracts:
Keynote
Title: Wave propagation in random multi-scale media and quantitative ultrasound imaging
Speaker: Laure Giovangigli
Affiliation: POEMS, CNRS, Inria, ENSTA Paris, Institut Polytechnique de Paris
Co-authors: Josselin Garnier (CMAP, CNRS, Ecole Polytechnique, Institut Polytechnique de Paris), Quentin Goepfert (CMAP, CNRS, Ecole Polytechnique & POEMS, CNRS, Inria, ENSTA Paris, Institut Polytechnique de Paris), Pierre Millien (Institut Langevin, ESPCI Paris, PSL University, CNRS), and Emile Parolin (Alpines, Inria, LJLL, Sorbonne Université)
Abstract: Due to the technical progress in sensors manufacturing during the last decades and the access to now extensive computational resources, the research in ultrasound imaging focuses now on refining the reconstruction algorithm and the underlying mathematical model. In soft tissues, the measured echoes come from numerous weakly contrasted unresolved scatterers. In this work we first aim at providing a mathematical framework for wave propagation in tissue-mimicking random multi-scale media. We derive a quantitative asymptotic expansion of the measured field with respect to the size of the scatterers using stochastic homogenization [Garnier, Giovangigli, Goepfert and Millien, Scattered wavefield in the stochastic homogenization regime, 2023]. We also present numerical simulations to illustrate our results. Secondly we use this asymptotics of the scattered field to justify the estimators of the effective speed of sound inside biological tissues introduced by A. Aubry [Bureau, Multi-dimensional analysis of the reflection matrix for quantitative ultrasound imaging, theses, Université Paris sciences et lettres, 2023]. By analyzing the dependence of the imaging functional with respect to the backpropagation speed, we build an estimator of the sound speed in the random multi-scale medium. We then confront our results with numerical simulations and experimental results.
Keynote
Title: Best Current Parallel in Time Methods for Parabolic and Hyperbolic Problems
Speaker: Martin J. Gander
Affiliation: Université de Genève, Section de Mathématiques
Abstract: Space-time parallel methods, also known more recently under the name PinT (Parallel in Time) methods, have a long history, but they have received a lot of attention over the past two decades. This is driven by the parallel hardware architectures that have now millions of cores, leading to saturation when parallelizing in space only. Parallelizing also the time direction is tempting, but this is very different from the space direction, because evolution problems satisfy a causality principle: the future is dependent on the past, and not the other way round.
I will show in my presentation that successful strategies for PinT methods depend strongly on the nature of the evolution problem. For hyperbolic problems, effective PinT methods are Domain Decomposition methods of Waveform Relaxation type, culminating in Unmapped Tent Pitching methods, ParaDiag methods, and also direct time parallel methods like ParaExp. Most of these methods can also be very effectively used for parabolic problems, but for such problems there are also highly successful multilevel methods, like Parareal and its variants. The currently best ones are however space-time multigrid methods. All these multilevel methods struggle however when applied to hyperbolic problems.
Keynote
Title: Impact of anisotropic mesh adaptation for turbulent flows in aeronautics. Towards the certification of numerical solutions ?
Speaker: Frédéric Alauzet
Affiliation: Inria GammaO
Abstract: This presentation will discuss recent progress made in anisotropic mesh adaptation for turbulent flow (RANS) simulations. We will focus on drag and lift prediction, and vortex dominated flows in aeronautics. First, we will present each step of the mesh-adaptive solution platform: the flow solver Wolf, the RANS error estimates (feature-based and goal-oriented will be compared), the local remesher Feflo.a and the solution interpolation method. The key point is to propose robust numerical methods that are compatible with extreme anisotropy, ie element ratios of 1:100000. We will describe how, in practice, the mesh adaptation loop is implemented and all the advantages of doing it in this way (multigrid type effect,free convergence study, …). In the presented examples, we will show the early capturing property of the mesh adaptation process on output functionals of interest, and, the fact that the mesh-convergence of the solution is achieved even in 3D. We will also emphasize the automaticity of the mesh adaptation process and its independence to the initial mesh. All these properties are a necessary first step towards the certification of numerical solutions.
Talk
Title: Minimization of spurious reflections for non regular traveling waves on non uniform grids
Speaker: Mamadou N’Diaye
Affiliation : Université Polytechnique Hauts-de-France (UPHF - CERAMATHS)
Co-authors: E. Creusé, J. Venel (UPHF - CERAMATHS), C. Hubert (UPHF - LAMIH) et N. Leconte (ONERA - Lille)
Abstract: Spurious wave reflections are likely to occur in explicit fast dynamics computations when coupling spatial discretizations of different types and steps. It corresponds to numerical pollution that does not correspond to physical reflections caused by geometry or material impedance changes at the coupling interface. To investigate this phenomenon, we consider a 1D pre-stretched bar test case in link with Split Hopkinson Bars (SHB) and the coupled FEM-FEM for space discretization combined with leapfrog method for time integration. In this talk, we describe an optimized explicit Runge-Kutta-Nyström (RKN) time integration method to minimize spurious wave generation, in the context of discontinuous wave propagation on nonuniform meshes. The proposed method, based on a one-dimensional analysis, consists in adjusting the parameter characterizing the RKN methods as a function of the CFL stability condition and the mesh discontinuity ratio used. It has the advantage of being non-intrusive, and can therefore be easily adapted to already existing codes. Numerical tests demonstrate the effectiveness of the method in 1D and 2D simulations.
Talk
Titre: Time Schemes for Solving Maxwell’s Equations in a Mesh Hybridization Strategy
Speaker: Xavier Ferrières
Affiliation: ONERA - The French Aerospace Lab, F-31055 Toulouse, France
Co-authors: V. Mouysset, S. Pernet, T. Volpert (ONERA - The French Aerospace Lab, F-31055 Toulouse, France)
Abstract: The efficient resolution of Maxwell’s equations remains a priority in the field of electromagnetic simulation due to the increasing complexity of the structures and systems to be studied or qualified. In the time domain, several schemes have been and are still being studied due to their advantages. In our case, for several years, we have believed that efficient simulation of a computational scene requires dividing it into multiple zones, each treated with the appropriate scheme. In this strategy, we focus on a global meshing of the scene into a Cartesian grid with polyhedral cell inclusions. This approach has the advantage of maximizing the number of Cartesian cells, which is particularly efficient for our methods, while allowing for zones adapted to curved geometries and refinement areas that account for the multi-scale aspects of the computational scene. In our presentation, we propose to showcase the multi-domain/multi-method strategy implemented by providing examples and studies conducted on the hybridization of certain schemes. We will then focus more specifically on the latest research carried out within the framework of theses, using FVTD (Finite Volume Time Domain) and CDO (Compatible Discrete Operator) schemes.
Talk
Titre : Conservation of divergence or rotational type constraints of hyperbolic systems with the discontinuous Galerkin method.
Speaker : Vincent Perrier
Affiliation : Project-team Cagire, Inria & UPPA
Abstract : A number of hyperbolic systems contain implicit conservations of the rotational or divergence of certain unknowns. Examples include the acoustic system (conservation of the velocity rotational), Maxwell’s system (conservation of the magnetic field divergence), or the magnetohydrodynamics system (transport of the magnetic field divergence). These constraints are generally difficult to preserve, and we generally resort to staggered schemes: historically, the MAC scheme or the Yee scheme, for example, or their finite element version, with Raviart-Thomas or Nédélec elements. The systematization of the study of these finite elements has been developed within the framework of finite element exterior calculation over the last thirty years. In this talk, starting from a simple problem (the long-time behavior of the acoustic system in finite volumes on triangular meshes), I will show that the classical discontinuous Galerkin spaces for vectors on triangular meshes can be put into a distributional de-Rham complex for which we can show the equivalence of the discrete and continuous cohomology groups, which is a property identical to the discrete conformal complexes involving the Nédélec and Raviart-Thomas elements. It will then be shown that we can develop approximation spaces on quadrangles on which the same type of property can be proved. It will further be proved that the classical discontinuous Galerkin method preserves rotationals and divergences, provided that the right approximation space is chosen, and under a diffusion direction assumption on the numerical fluxes. Finally, theory will be illustrated by numerical results obtained on 2D Maxwell equations, on the acoustic system, and on the induction equation.
Talk
Title: Cancellation Integration Scheme for the Magnetic Boundary Integral Operator on Curved Elements and Application to the Accurate Computation of the Radar Cross Section
Speaker: Matthias Barray
Affiliation: CEA Cesta
Co-authors: Agnès Pujol (CEA Cesta), Emanuele Arcese (CEA Cesta) and Francis Collino (CEA Cesta)
Abstract: The general issue of this paper concerns the accurate computation of the Radar Cross Section (RCS) of an object made of some homogeneous dielectric materials. The RCS is computed here by solving the boundary integral equation: the PMCHWT. Its discretization is done with a Galerkin method using the well-known lowest-order Raviart-Thomas (RT) divergence-conforming basis functions. In addition, we use here a geometric approximation of the scattering surface with quadratic triangles. The PMCHWT weak formulation involves strongly singular integrals related to the magnetic boundary integral operator for which the design of accurate quadrature formulae is not an easy task.
In this work, we propose an accurate, efficient and easy-to-implement algorithm for the evaluation of strongly singular integrals on quadratic triangles. Our integration scheme is based on a singularity cancellation technique accounting for some geometric considerations between vector basis functions and curved elements. We show, in particular, that the integral singularity is of the kind 1/R and not 1/R² as might appear at first glance when looking at magnetic boundary integral operator. This is made possible by splitting the double surface integral into two parts, each of which involves 1/R singularity thus allowing us to use the well-known Duffy’s transform. As a result, the function to be integrated is continuous, making it possible to use a classical Gauss quadrature rule over 1D integration domains. An additional favorable point of the proposed scheme is that it is independent of the form of the basis functions, meaning the scheme can be easily generalized to high-order Raviart-Thomas functions, for example.
Moreover, we also present a method, based on a refinement technique, for validating integration schemes when the exact value of the integral to be computed is not known. Some numerical results showing the efficiency of the proposed integration scheme compared to alternative techniques in the literature will be presented. We conclude with some electromagnetic benchmarks wherein an accurate computation of the RCS is required.
Talk
Title: : 1st kind BEM applied to non-destructive eddy current testing
Speaker: Edouard Demaldent
Affiliation: Université Paris-Saclay, CEA, List, F-91120, Palaiseau, France; E-mail: edouard.demaldent@cea.fr
Abstract: The Boundary Element Method (BEM) is suitable for many eddy current testing (ECT) configurations, in particular to help diagnose the integrity of heat exchangers in the nuclear industry. CEA-LIST is developing a BEM code dedicated to these applications, integrated into the CIVA software platform, whose target users are non-destructive testing experts. In this presentation, we will begin by introducing the application context of ECT inspection. This is characterized by an asymptotic low-frequency, high-conductivity regime in a zone of interest whose characteristic size is inversely proportional to the skin depth, so as to ensure good sensitivity to the presence of a defect. We will develop the BEM variant of Maxwell’s transmission problem adapted to this regime and highlight the simplification of the underlying linear system to be solved [Bonnet & Demaldent, CAMWA 2023]. We will then discuss the R&D activities carried out at CEA-LIST around the ECT-BEM, such as the use of high-order boundary elements.
Talk
Title: Full Helmholtz decomposition on non simply connected domains, application to 1st kind BEM for low-frequency electromagnetics
Speaker: Marc Bakry
Affiliation: Université Paris-Saclay, CEA, List, F-91120, Palaiseau, France; E-mail: marc.bakry@cea.fr
Abstract: We propose a new approach for the computation of the full Helmholtz decomposition for general, eventually open, non simply connected domains. For such geometries, it is well-known that a vector field can be decomposed into a divergence-free component, a curl-free component and a harmonic component. To that purpose, we use the quasi-Helmholtz projector on the harmonic subspace. By computing a basis of its range, we obtain directly the coefficients of the expansion of the so-called global loops on the discrete Raviart-Thomas (or RWG) subspace. This basis can be computed in two ways : either we can use a low-rank SVD (using an iterative algorithm), or we can use the so-called Randomized Range Finder algorithm which very easy to implement and very efficient in practice. Application examples with both algorithms are given for the low-frequency Electric Field Integral Equation and for real-life examples in the context of the Eddy current nondestructive testing.
Talk
Title: Wave and spectral solvers with self-gravitation for radially symmetric adiabatic backgrounds in helioseismology
Speaker: Lola Chabat
Affiliation: UPPA, Inria, Makutu, TotalEnergies, UMR CNRS 5142
Co-authors: Ha Pham, Florian Faucher, Hélène Barucq (Inria, Makutu, TotalEnergies, UPPA, UMR CNRS 5142) and Damien Fournier (Max Planck Institute for Solar System Research)
Abstract: Small acoustic solar waves can be modeled with the linearized equations derived by Lynden-Bell and Ostriker (1967). Without Cowling’s approximation, this system of equation consists of an equation of motion defined on the Sun and Poisson’s equation with vanishing source in the atmosphere, and has as unknowns, the Lagragian displacement and gravity perturbation. It is closed by a vanishing-at-infinity condition for the gravity perturbation, and a closed boundary condition for the displacement at the surface. Radial symmetry is exploited to decouple the problem to each harmonic mode and allows to impose the exact Dirichlet-to-Neumman condition for gravity perturbation. For wave solver, we implement and compare between HDG and CG method; for the eigensolver, we consider IPDG method. These problems are particularly challenging with standard solar model-S background, due to the rapid drop of density and sound speed in near-surface layer. For this model and Dirac source, we observe that the HDG method, when employed with a judicial choice of stabilization, is more robust and less sensitive to mesh refinement than CG. We validate both solvers by comparing with Gyre software and HMI solar spectrum. The eigenvalues computed with IPDG agree with the numerical ones computed by Gyre, and show agreement with the location of peaks in the Green’s kernel (indicading maximum power) computed with HDG. These all agree with HMI observed eigenvalues at low frequencies.
Talk
Title: A Quasi-Trefftz Method for the Iterative Solution of Time-Harmonic Wave Problems based on the Flux Reconstruction Method
Speaker: Matthias Rivet
Affiliation: Onera Toulouse, UPPA, Inria, TotalEnergies, Makutu, UMR CNRS 5142
Co-authors: Sébastien Pernet (Onera, Toulouse) and Sébastien Tordeux (UPPA, Inria, TotalEnergies, Makutu, UMR CNRS 5142)
Abstract: In this talk, we will consider the problem of time-harmonic wave propagation in large domains for which classical numerical methods lead to memory-prohibitive direct solution, and matrices which are poorly suited to iterative algorithms. Then, we introduce a Trefftz approach, which can be seen a Discontinuous Galerkin formulation whose basis functions are actual solutions of the equations, and is well adaptable to iterative solution. Plane Waves are classically chosen as basis functions, unfortunately leading to conditioning and precision limitations. Thus, we propose a quasi-Trefftz approach based on a Flux Reconstruction solver and local polynomial boundary conditions, allowing to define well-conditioned basis functions. Properties, optimisation and calibration of this local solver will be investigated through numerical convergence studies, and will demonstrate the robustness and precision of this methodology in HPC context.
Talk
Title: The importance of an efficient Helmholtz solver for modelling plasma discharges at atmospheric pressure
Speaker: Marie Bibal
Affiliation: ONERA - The French Aerospace Lab, F-31055 Toulouse, France
Abstract: The objective is to present the models on which the simulation of plasma discharges at atmospheric pressure rely and the link with a Helmholtz solver. First, the importance of photo- ionization in the development of the discharge and its modeling will be explained. The classical approach for computing the photo-ionization source term relates on an integral over the entire discharge volume, which is computationally expensive. To accelerate the simulation, various approximations have been developed to reduce this computational cost. Among them, the method based on solving a set of Helmholtz equations has emerged as one of the most effective. This is the numerical approach adopted in the COPAIER plasma solver, developed at ONERA, which will be detailed.
Talk
Title: Recent Developments in Waves Simulation at Airbus
Speaker: Guillaume SYLVAND
Affiliation: Airbus Central R&T
Abstract: Wave propagation is at the heart of many physical aspects involved in aircraft development at Airbus. Thus, aeroacoustics can simulate the propagation of sound around and inside an aircraft, reducing the noise level affecting passengers, ground crew working on the aircraft and populations living around airports. On the other hand, electromagnetism governs the modeling of the operation and interactions between all the antennas equipping modern aircraft: an A350, for example, carries more than 50 antennas, meaning more than 2,500 possible interactions, which would have to be modeled at the design stage of the aircraft to ensure the proper operation of the whole. These two physics lead to solving the same equation, the wave equation, on problems that are potentially very large. To this end, Airbus Central R&T (in association with Inria and Cerfacs in the CONCACE joint team) is continuously developing high-performance solvers adapted to current and future computing machines. In this presentation, we present three current research directions: first, for aeroacoustics in heterogeneous media, we are interested in the use of Quasi-Trefftz based Discontinuous Galerkin Method. Then, in formulations coupling surface and volume finite elements, we work on the development of composable HPC solvers capable of handling linear systems mixing dense and sparse parts. Finally, in the case of homogeneous propagation media, we seek to improve low-rank hierarchical solvers.
Talk
Title: Asymptotic expansion and pseudodifferential calculation methods for wave propagation and reflection in a harbor.
Speaker: Olivier Lafitte
Affiliation: Université Sorbonne Paris Nord
Co-authors: E. Audusse (Université Sorbonne Paris Nord) and C. Sulem (Department of Mathematics, Toronto University)
Abstract: Linearized wave propagation leads to a system of wave equations involving the Dirichlet to Neumann (DtN) operator of the potential equation. The pseudodifferential system used to find DtN operator then allows us to find the linearized swell in an asymptotic taking into account the successive derivatives of the function characterizing the bottom. These results are valid for shallow, intermediate and deep water.
Talk
Title: Optimization of equivalent circuit models for metal-patterned metasurfaces.
Speaker: Ilyes Moufid
Affiliation: CEA CESTA
Coa-Authors: P. Aguilera (CEA Cesta) et J. Labat (CEA Cesta)
Abstract: To design high-absorption coatings, we focus on the characterization of metasurfaces composed of homogeneous planar materials with periodic metallic inclusions. Their modeling is carried out analytically using an equivalent circuit, assuming that the incident plane wave has a wavelength much larger than the characteristic size of the patterns. We performed a numerical study to assess the validity of the circuit models defined by the pattern geometry. Based on the obtained validity domain, we successfully carried out a shape optimization of a metasurface using a metallic frequency-selective surface. Finally, we aim to extend this work to broadband metasurfaces.
Talk
Title: Fast solution of a nonlinear eigenvalue problem from photonic crystal fiber applications discretized by a boundary element method.
Speaker: Jean-René Poirier
Affiliation: INP-ENSEEIHT - LAPLACE, Toulouse
Abstract:
The computation of Photonic Crystal Fiber with a waveguide mode solver based on boundary integral equation gives rise to a nonlinear eigenvalue problem to solve.
Several strategies for solving this one can be used and a single non-linear resolution leads to solve several ill conditioned linear systems.
H-matrices can be used in order to build a preconditioner, accelerate and increase the accuracy of the computations.
The easiest strategy, that can illustrate the main difficulties, is to solve the problem using Muller’s method.
This one requires a rather precise knowledge of the solution as a starting point.
We then look at more recent techniques based on contour integrals or a rational interpolant that can be used to compute several eigenmodes simultaneously and considerably reduce the volume of computations.
A less knowledge of the solution is needed (no close starting point) and the computation of several solutions can be done. In addition no computation with a matrix close to the singularity is needed.
The numerical experiments show that the rational interpolant is the most efficient for solving this problem.
Talk
Title: Dispersion correction for finite difference approximations of Helmholtz equation.
Speaker: Pierre-Henri Cocquet
Affiliation: Université de Pau et des Pays de l’Adour, Laboratoire SIAME.
Abstract: This talk will present a dispersion correction method for finite difference schemes applied to the Helmholtz equation. The latter is based on the introduction of a shifted wavenumber in the FD stencil that can be determined in closed form by minimizing the dispersion error. We will apply this technique on some specific FD stencil and show, though some numerical experiments, that it reduces the relative error for large enough numbers of grid points per wavelength.





